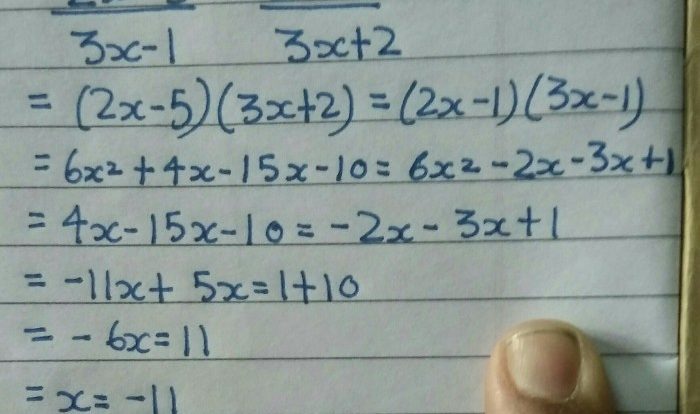Fundamentals of differential equations and boundary value problems 7th edition – Fundamentals of Differential Equations and Boundary Value Problems, 7th Edition embarks on an illuminating journey into the realm of differential equations, providing a comprehensive exploration of first-order, higher-order, and systems of differential equations, along with boundary value problems. This seminal work unveils the significance of differential equations in modeling real-world phenomena and empowers readers with the analytical tools to solve complex problems in various scientific disciplines.
Delving into the intricacies of differential equations, this text unravels the fundamental concepts, methods, and applications that underpin this captivating field. From understanding the behavior of simple first-order equations to tackling the complexities of higher-order and systems of differential equations, readers embark on a transformative learning experience that equips them with the knowledge and skills to excel in this challenging subject.
Fundamentals of Differential Equations and Boundary Value Problems
Differential equations are mathematical equations that involve derivatives of unknown functions. They are used to model a wide range of physical, biological, and engineering systems.
First-Order Differential Equations
First-order differential equations are equations that involve the first derivative of the unknown function. They can be solved using a variety of methods, including separation of variables, integrating factors, and exact equations.
Applications of First-Order Differential Equations
- Population growth and decay
- Radioactive decay
- Mixing problems
- Heat transfer
Higher-Order Differential Equations: Fundamentals Of Differential Equations And Boundary Value Problems 7th Edition
Higher-order differential equations are equations that involve derivatives of the unknown function of order greater than one. They can be solved using a variety of methods, including the method of undetermined coefficients, variation of parameters, and Laplace transforms.
Applications of Higher-Order Differential Equations
- Vibrating strings
- Elastic beams
- Electrical circuits
- Chemical reactions
Systems of Differential Equations
Systems of differential equations are equations that involve more than one unknown function. They can be solved using a variety of methods, including matrix methods, the Laplace transform, and numerical methods.
Applications of Systems of Differential Equations, Fundamentals of differential equations and boundary value problems 7th edition
- Predator-prey models
- Epidemic models
- Economic models
- Mechanical systems
Boundary Value Problems
Boundary value problems are differential equations that are subject to additional conditions on the unknown function at the boundaries of the domain. They can be solved using a variety of methods, including the method of separation of variables, the Green’s function method, and the finite element method.
Types of Boundary Value Problems
- Dirichlet boundary conditions
- Neumann boundary conditions
- Cauchy boundary conditions
- Mixed boundary conditions
Applications of Differential Equations
Differential equations are used in a wide variety of fields, including physics, engineering, biology, and economics. They are used to model a variety of phenomena, including population growth, heat transfer, fluid flow, and chemical reactions.
Examples of Applications of Differential Equations
- Predicting the weather
- Designing bridges and buildings
- Developing new drugs
- Modeling the economy
Numerical Methods for Differential Equations
Numerical methods are used to solve differential equations that cannot be solved analytically. These methods approximate the solution of the differential equation using a computer. There are a variety of numerical methods available, including the Euler method, the Runge-Kutta method, and the finite difference method.
Advantages and Disadvantages of Numerical Methods
| Advantages | Disadvantages |
|---|---|
| Can be used to solve a wide variety of differential equations | Can be computationally expensive |
| Can be used to solve differential equations with complex boundary conditions | Can be less accurate than analytical methods |
| Can be used to solve differential equations that are too difficult to solve analytically | Can be unstable |
Expert Answers
What are the key concepts covered in Fundamentals of Differential Equations and Boundary Value Problems, 7th Edition?
This comprehensive text covers first-order differential equations, higher-order differential equations, systems of differential equations, boundary value problems, and numerical methods for solving differential equations.
How does this book approach the teaching of differential equations?
Fundamentals of Differential Equations and Boundary Value Problems, 7th Edition adopts a balanced approach, combining theoretical foundations with practical applications. It provides clear explanations of concepts, step-by-step solution methods, and real-world examples to foster a deep understanding of the subject.
What are the benefits of using this book as a resource for differential equations?
This book offers a wealth of benefits, including comprehensive coverage of the subject matter, engaging writing style, numerous solved examples, practice exercises, and thought-provoking discussion questions that enhance learning and retention.