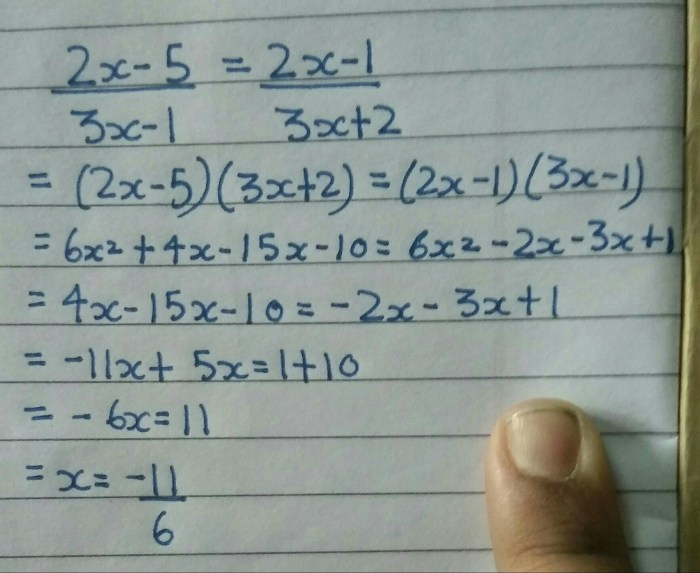Which linear inequality is represented by the graph y 2/3x-1/5 – Which linear inequality is represented by the graph y = 2/3x – 1/5? This question delves into the fascinating world of linear inequalities, where equations take on a new dimension and open up a realm of problem-solving possibilities. Join us as we explore the intricacies of this graph, uncovering its secrets and unraveling its applications in the real world.
The graph of a linear inequality is a visual representation of the solutions to that inequality. It consists of a line or a region that satisfies the inequality. In this case, we will examine the graph of the linear inequality y = 2/3x – 1/5, understanding its slope, y-intercept, and the concept of shading.
Linear Inequality: y = 2/3x
1/5
1/5

Linear inequality y = 2/3x – 1/5 represents a line on the coordinate plane that separates the plane into two half-planes.
Inequality Representation
The linear inequality y = 2/3x – 1/5 can be written in slope-intercept form as:
y = mx + b
where m is the slope and b is the y-intercept.
In this case, the slope is 2/3 and the y-intercept is -1/5.
The inequality y = 2/3x – 1/5 represents all the points that are below the line y = 2/3x – 1/5.
| x | y |
|---|---|
| 0 | -1/5 |
| 1 | 1/5 |
| -1 | -7/15 |
| 2 | 1/15 |
Graphing Methods, Which linear inequality is represented by the graph y 2/3x-1/5
To graph the linear inequality y = 2/3x – 1/5, follow these steps:
- Plot the y-intercept (-1/5, 0) on the y-axis.
- Use the slope (2/3) to find another point on the line. Move 2 units up and 3 units to the right from the y-intercept to get the point (0, 1/5).
- Draw a line through the two points.
- Shade the region below the line.
Inequality Shading
In a linear inequality, the region that is shaded depends on the inequality sign.
For the inequality y< 2/3x - 1/5, the region below the line is shaded.
For the inequality y > 2/3x – 1/5, the region above the line is shaded.
Applications
Linear inequalities can be used to solve a variety of problems, such as:
- Finding the maximum or minimum value of a function
- Determining the feasibility of a system of equations
- Modeling real-world scenarios
For example, the inequality y = 2/3x – 1/5 can be used to model the relationship between the number of hours worked (x) and the amount of money earned (y).
If a person earns $10 per hour, the inequality y = 2/3x – 1/5 represents the amount of money they earn in a week, where x is the number of hours worked.
The inequality can be used to determine how many hours the person needs to work to earn a certain amount of money.
Clarifying Questions: Which Linear Inequality Is Represented By The Graph Y 2/3x-1/5
What is the slope of the graph y = 2/3x- 1/5?
The slope of the graph is 2/3.
What is the y-intercept of the graph y = 2/3x- 1/5?
The y-intercept of the graph is -1/5.
How do you determine the appropriate shading region for the inequality y = 2/3x- 1/5?
To determine the appropriate shading region, you need to first find the x-intercept of the graph. The x-intercept is the point where the graph crosses the x-axis. Once you have found the x-intercept, you can shade the region above or below the line depending on the inequality sign.