Introducing the Pythagorean theorem study guide answer key, an invaluable resource for mastering this fundamental mathematical concept. This guide provides a comprehensive overview of the Pythagorean theorem, its applications, and various proofs, empowering you to tackle any problem with confidence.
Delving into the intricacies of the theorem, we explore its real-world applications in construction, engineering, and surveying, demonstrating its practical significance. Additionally, we delve into the concept of Pythagorean triples and their utility in simplifying calculations.
1. Pythagorean Theorem Statement and Formula
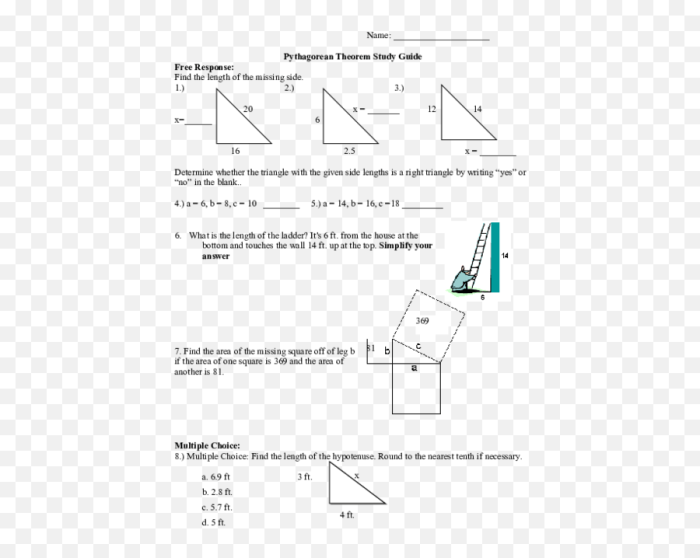
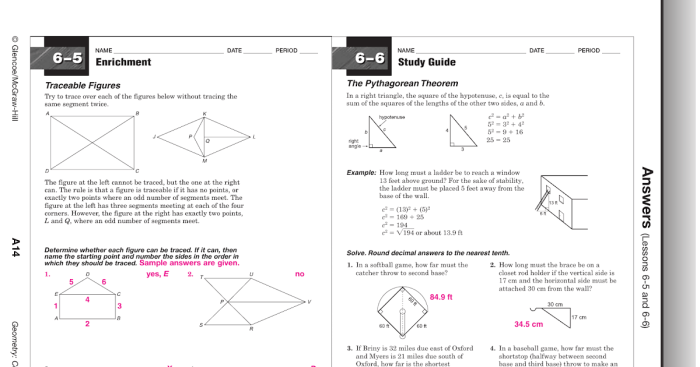
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
The Pythagorean theorem formula is: “` a^2 + b^2 = c^2 “` where a and b are the lengths of the two shorter sides of the triangle and c is the length of the hypotenuse.
2. Applications of the Pythagorean Theorem
The Pythagorean theorem is used in a wide variety of applications, including:
- Construction: To determine the length of rafters, joists, and other building components.
- Engineering: To calculate the forces and stresses in structures.
- Surveying: To determine the distance between two points.
- Navigation: To calculate the distance between two points on a map.
3. Pythagorean Triples, Pythagorean theorem study guide answer key
Pythagorean triples are sets of three positive integers that satisfy the Pythagorean theorem.
The most common Pythagorean triples are:
- (3, 4, 5)
- (6, 8, 10)
- (5, 12, 13)
Pythagorean triples can be used to simplify calculations involving the Pythagorean theorem.
4. Proofs of the Pythagorean Theorem
There are many different proofs of the Pythagorean theorem.
One of the most common proofs is the geometric proof, which uses the following diagram:
[Diagram of a right triangle with squares drawn on each side]
The geometric proof shows that the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
Another common proof is the algebraic proof, which uses similar triangles.
5. Extensions of the Pythagorean Theorem
The Pythagorean theorem can be extended to right triangles in three dimensions.
The Pythagorean theorem for right triangles in three dimensions is:
“`a^2 + b^2 + c^2 = d^2“`where a, b, and c are the lengths of the three shorter sides of the triangle and d is the length of the hypotenuse.
The Pythagorean theorem can also be extended to non-right triangles.
Questions Often Asked: Pythagorean Theorem Study Guide Answer Key
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
How is the Pythagorean theorem used in real-world applications?
The Pythagorean theorem is used in a wide range of applications, including construction, engineering, and surveying. It can be used to calculate the height of buildings, the length of bridges, and the distance between objects.
What are Pythagorean triples?
Pythagorean triples are sets of three numbers that satisfy the Pythagorean theorem. Common Pythagorean triples include (3, 4, 5), (6, 8, 10), and (5, 12, 13).